Make Better Space

남세동 대표의 딥러닝 질문리스트 중 마지막으로 다뤄볼 내용은 optimizer의 momentum과 ADAM 알고리즘이다

(그 외 내용은 다른방식으로 다루었거나 다룰 예정)

Adam은 입문단계에서 묻지도따지지도말고 국룰이라 momentum과 Adam은 많이들 익숙한 내용일 것이다

Adam 논문은 2022년 현재 피인용수 10만 무렵이지만,

너무 trivial 하여 인용하지않았거나 논문으로 발간되지 않은 사용사례가 그 몇배는 될 것으로 예상한다

Andrew Ng 님의 강의 Gradient Descent With Momentum (C2W2L06) 를 기초로

수식과 함께 정확하게 정리해보자

6. Optimizer에서 momentum은 무엇인가요? 

a. momentum을 수식으로 적어본다면 어떻게 되나요? 

기본적인 gradient descent 에서는 optimizer(최적화 알고리즘) 에 의해 모델의 오차가 줄어들도록 설정한다

이 때, learning rate가 작으면 학습이 너무 오래걸리거나 local minima에 빠질 수 있고,

learning rate가 크면 학습이 overshooting 또는 diverge 되는 문제를 야기할 수 있다.

이를 극복하기 위해서 momentum은 gradient가 일관적인 방향으로 조금 더 빠른 최적화를 수행하도록하는 term이다

momentum의 수식을 이해하기 위해 먼저 Exponentially Weighted Moving Average (지수가중이동평균)의 개념을 짚고 넘어가자

데이터의 이동평균을 구하기 위해 현재 평균값과 새로 추가되는 데이터를 β만큼 가중치를 준다면

V(t) =  β*V(t-1) + (1- β)*θ(t) 로 표현할 수 있다.

다시말하면 β 값이 클수록 직전의 평균값에 더 큰 가중치를 주는 것이다.

이 때 V(t)≈ avg. of 1/(1-β) days 라는 성질을 가진다. 예를 들어 β=0.9라면 V(t)는 10일치의 평균과 유사하다.

더 긴 기간의 이동평균을 계산하므로 더 smooth 한 V(t) 그래프를 얻을 수 있다.

momentum 의 정의는 gradient의 지수가중이동평균을 구하는 것이다

위에서 적은 수식과 마찬가지로 weight 또는 bias 의 gradient 를 

V(dw) =  β*V(dw) + (1-β)*dw 로 정의하고

learning rate α를 적용해서 W=W-αV(dw) 로  모델을 업데이트할 수 있다.

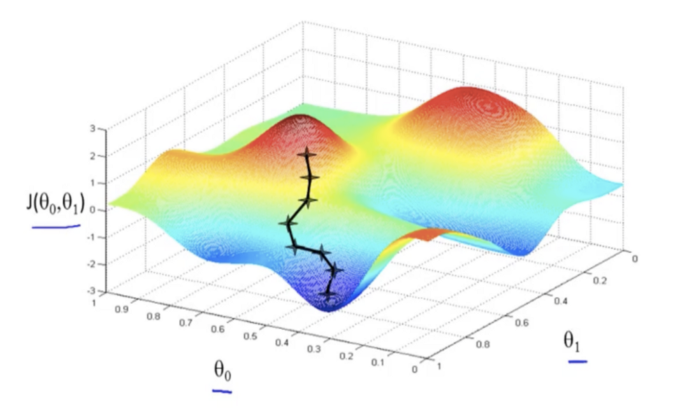
예를 들어 cost function이 아래 그림과 같다면

수직방향으로의 이동폭은 줄이는 동시에, 수평방향(오른쪽)으로의 이동폭을 늘여야 빠르고 정확하게 모델이 최적화된다.

momentum은 gradient의 이동평균을 이용해서 "이전에 가던 방향"으로의 학습을 빠르게 만들어 준다.

learning rate 와 momentum의 설정에 의한 모델 최적화 결과를 시각화하면 보다 직관적인 이해가 가능하다

( https://distill.pub/2017/momentum/ )

momentum을 이용하면 모델이 global minima와 거리가 먼 초기 단계에서는 학습속도를 빠르게 진행시키고

학습이 진행될수록 momentum이 작아지면서 정밀한 fine tuning이 가능해진다.

b. Adam은 어떻게 동작하나요?

Adam은 momentum 방식과, RMSProp(Tieleman & Hinton, 2012)을 결합한 최적화 알고리즘이다.

참고로 RMSProp는 제곱항과 제곱근을 이용해서 아래와 같이 계산하는 방식이다.

기본적인 원리는 모멘텀과 크게 다르지않다.

Adam논문에서 쓰인 알고리즘을 바로 보자

여기서 β1로 계산한 m_t 가 momentum 파라미터이고,

β2 와 제곱항으로 계산한 v_t가 RMSProp 에서 차용한 파라미터이다.

bias correction 은 크게 신경쓰지않아도 되고..

모델 업데이트 과정에서 momentum과 RMSProp의 업데이트 방식을 결합한 것을 볼 수 있따.

Adam은 이처럼 기존의 아이디어들을 개선한 결과물이지만

굉장히 좋은 성능으로 딥러닝 입문단계나 모델 개발과정에서 고민을 줄여주는 고마운 알고리즘이다

파이썬 컴프리헨션(comprehension) 문법은 

좋은 코드인 파이썬스러움(Pythonic)의 대표적인 문법 중 하나로 코드의 간결성과 성능을 모두 높일 수 있다.

리스트 컴프리헨션(List Comprehension)을 만들어보자

(참고자료)

제대로 파이썬 : https://wikidocs.net/22805 ,

티베트 모래여우님 블로그 : https://tibetsandfox.tistory.com/25?category=885924)

TASK : 1부터 10까지 정수를 포함하는 리스트를 만든다

(1) 리스트 컴프리헨션

list1 = [x for x in range(1,11)]

(2) list() 함수를 이용 

list2 = list(range(1,11))

(3) for 반복문 이용

list3 = []
for i in range(1, 11):
    list3.append(i)

예시처럼 간단한 경우에는 list()함수를 써도 좋지만, list()는 어디까지나 리스트 형식으로 반환하는 기본함수이므로 복잡한 데이터를 정의하기에 적합한 방식은 아니다.

for문은 여러 조건을 쉽게 추가할 수 있지만, 계산도 오래걸리고 코드를 길고 복잡하게 만드는 주범이니 역시 데이터가 커질수록 좋지않다.

TASK : 1부터 10까지 정수 중, {5보다 작은 수,짝수} 쌍을 포함하는 리스트를 만든다

list4 = [(x, y) for x in range(1, 11) for y in range(1, 11) if x < 5 if y % 2 == 0 ]

컴프리헨션 문법으로 코드를 간결하게 만드는 장점을 보여주는 좋은 예제이다.

이처럼 컴프리헨션에서는 for 과 if 를 연속해서 적어주는 것으로 조건을 중첩하여 적용할 수 있다.

중첩된 for문의 실행순서는 왼쪽부터, if문은 for문 다음에 적어준다는 규칙을 알아두자.

그리고 마지막으로 프로그래머스 코딩테스트 연습문제 중 'k번째 수' 예제에 적용해보자

TASK: 배열 array의 i번째 숫자부터 j번째 숫자까지 자르고 정렬했을 때, k번째에 있는 수를 구하려 합니다.

#부끄럽지만 내가 예전에 썼던 코드
def solution(array, commands):
    answer = []
    for i,j,k in commands:
        sliced = sorted(array[i-1:j])
        answer.append(sliced[k-1])
    return answer

#컴프리헨션을 이용한 리스트
def solution(array, commands):
    answer = [ sorted(array[i-1:j])[k-1] for (i, j, k) in commands ]
    return answer

이렇게 for 문을 리스트 컴프리헨션으로 적어주면 깔끔하게 정리가 가능하다.

다시보니 처음 짰던 코드에서는 sliced 라는 중간 데이터를 만든 것도

실험용 데이터 분석을 하다보니 더블체크를 하려고 생긴 습관인데

대규모 연산이나 상용프로그램을 짤때는 메모리 낭비가 발생하지 않도록 유의해야겠다.

남세동 대표님의 질문 시리즈 5번째는 Loss Surface에 관한 질문이다

우리말로는 손실평면 으로 표현하는 문헌도 있지만 대체로 원어를 그대로 사용하는듯하다.

Loss Surface는 시각화 결과니까 크게 신경쓰지않고 직관적으로 받아들이는 경우가 많은데 좀더 자세히 알아보자

5. Loss surface에서 z축은 무엇인가요? 

a. x축, y축은 무엇일까요? 

먼저 loss surface 라는 용어의 정의를 찾아보자

[loss surface]
A graph of weight(s) vs. loss. Gradient descent aims to find the weight(s) for which the loss surface is at a local minimum.
@ https://developers.google.com/machine-learning/glossary

너무 간단하다...ㅎㅎ

일단 질문에서 x,y,z축을 질문했으니 loss surface는 3D 평면을 의미한다고 생각하자.

Loss Surface는 머신러닝 모델의 파라미터 값에 따라 loss (또는 cost)의 변화를 시각화하는 표현방법이다.

잘알고있듯이 gradient descent 방법은 오차의 gradient를 최소화하는 방향으로 모델을 업데이트하므로,

오차를 2차원 곡선 또는 3차원 평면(Loss Surface)에 시각화하여 모델이 업데이트되는 경로를 쉽게 시각화 할 수 있다.

여기서 z축은 loss function 값이다.

따라서 현재 지점에서 z값이 작아지는 gradient 방향이 모델이 업데이트 되는 방향이다

반면 x축과 y축을 정하는 것은 조금 복잡하다.

모델의 파라미터에 따른 loss를 표현한다고 했는데 딥러닝에서 파라미터(=가중치)의 갯수는 적어도 수만개이고, GPT-3 같은 대규모 모델은 천억개가 넘는 파라미터를 가지고 있다.

따라서 시각화를 위해서 1개(2D) 내지는 2개(3D)의 변수를 선정해야한다.

이를 위해

Li et al.,(2018) "Visualizing the Loss Landscape of Neural Nets" @ NeurIPS 2018

논문에서 제안하는 방법으로는

현재까지 학습된 모델을 좌표상 원점인 지점 θ* 으로 설정하고,

weight space에서 선택한 랜덤벡터 δ(델타)와 η(에타) 와 좌표의 두 점 α,β에 대해서

f(α,β) = L( θ* + αδ + βη ) 으로 손실함수 값을 구한다.

그 결과, x=α, y=β, z= f(α,β)  로 3차원 평면을 투영할 수 있다.

여기서 궁금한점이 생긴다. 그냥 랜덤으로 x축과 y축 파라미터를 골랐다고?논문에서 설명한 방법을 응용하면서 자세한 설명을 덧붙인 Javier의 블로그 를 참고해봤다.1. 왜 PCA를 사용하지 않는가? > 꼭 PCA를 통해 최적화(optimized)된 벡터를 이용할 필요는 없다2. 2개의 랜덤벡터가 직교하여 평면을 만들 수 있다고 가정할 수 있는가?> space의 차원이 커질 수록, 서로 다른 두 벡터가 직교할 확률은 1에 충분히 가까운 것이 수학적으로 설명된다

 다시 말하면 이 방식으로 구한 loss surface는 high dimension 모델의 오차함수를 2차원으로 슬라이스한 것과 같다.

이런 이유로 보통 loss surfcae는 개념적 설명을 돕기위한 시각화 방법이지 정확한 표현이 아니므로 굳이 고해상도 그림을 만들 필요는 없다.

하지만 위 블로그를 만든 Javier 의 losslandscape 프로젝트는 loss surface의 해상도를 극한으로 끌어올려서

마치 어느 극한지형을 보는 듯한 예술작품을 만들었으니 잠시 감상해보자

b. Loss surface가 불연속일 수도 있을까요?

이 질문은 자료를 찾아도 나올법한 질문이 아니라서 나름대로의 답안을 생각해봤다.

실제로 우리가 보는 figure는 임의의 해상도로 정의된 좌표에서 x=α, y=β, z= f(α,β) 로 나타냈으므로 당연히 불연속하다.

그러나 loss surface의 정의에 따르면 뉴럴넷 모델이 가지는 고차원의 loss function 그래프 중 3-D subspace 이다.

예를 들어 본래의 모델에서 첫번째 2가지 파라미터를 선택하여 loss surface를 만든다고 하면original dataset : p1=[1,2,0,0,0] p2=[1,2,5,5,5] p3=[1,2,7,7,7]original loss : L1=[0.3] , L2=[0.4] , L3=[0,1]

on surface: f(1,2) = SUM(L1,L2,L3) 의 꼴로 나올 것이다. (이부분 굉장히 자신없음)

이 경우에 본래의 loss function 이 (일반적으로 미분가능해야하므로) 연속하므로,

loss surface 역시 연속할 것이라고 생각한다.

사실 이 글의 제일 첫 단계에서 loss surface는 시각화를 위해 3D로 차원축소한 그래프로 정의했는데이 경우 loss surface의 함수적 특성에 대해 디테일하게 생각할 필요가 있을지 잘 모르겠다.

===

이번 편은 질문이나 자료가 많이 없는 주제라서, 답에 대한 충분히 확신을 가지진못하면서 마무리한다..

추가로 여유가 된다면, Nguyen and Hein의 2017 ICML 논문 "The Loss Surface of Deep and Wide Neural Networks" 에 관련된 자료를 찾아보는 것도 좋겠다.

왜 딥러닝이 local minima 문제에 잘 빠지지않는 이유로 '실제로 대부분은 global minima 또는 그 가까이에서 수렴한다. 라는 이론을 제시해주었고 

남세동 대표님의 딥러닝 신입개발자에게 묻는 질문 시리즈의 4번째는 mini-batch (미니배치) 사용에 대한 질문이다.

다행히도(?) 얼마전에 코딩하면서 자료도 찾아보고 테스트해봤던 내용이지만

이번 기회에 깔끔하게 정리해본다

4. Mini-Batch를 사용하는 이유가 무엇인가요? 

a. 사양이 허락한다면 Mini-Batch보다 (Total) Batch가 좋을까요? 

기본적으로, 딥러닝 모델을 학습하기 위한 대용량의 데이터는 GPU 메모리보다 큰 경우가 일반적이다.

이 때문에 전체 데이터를 mini-batch(미니배치)로 나누어서 여러번 학습을 나누어서 수행한다. 이 나누어진 횟수를 iteration 이라고 부른다.

학습과정에서 1 epoch 은 이 미니배치로 나누어진 전체 데이터가 1번 학습되었을 때를 뜻한다.

통상적으로  미니배치의 사이즈는 2^n 으로 정의하는데 메모리 활용 측면에서 유리함이 있다고 한다 (더 구체적으로 알 필요는 없을듯하다)

그러면 toy example이나 실무에서 데이터가 크지않은 경우에는 굳이 미니배치를 쓰지 않아도 될까?

이론적으로나 본인의 경험으로나 그렇지 않았다.

메모리 가용범위 내에서 배치 사이즈를 늘릴 경우 epoch을 돌리는 속도는 당연히 증가한다.

하지만 전체 데이터를 사용하는 모델(BGD)의 성능은 미니배치를 사용할 때 보다 현저히 낮게 나왔다.

BGD 모델의 epoch을 단순히 늘리는 것으로는 성능이 개선되지도 않고 오버피팅의 문제도 발생할 수 있다.

같은 데이터를 학습시켰는데 왜 모델의 성능이 차이날까?

미니배치만큼 더 작은 local 데이터에 대해서 더 많이 (iteration 수 만큼) 학습하기때문이다.

배치크기가 크면 그만큼 큰 데이터셋에서 계산된 gradient 의 평균치를 모델이 학습한다. 이 때는 여러번의 epoch으로 학습하더라도 계속 같은 데이터를 사용하므로 데이터셋의 local minima에 빠질 수 있다.

이를 잘 나타낸 카카오블로그의 그림을 보자.

반면 극단적으로 배치 사이즈=1 인 경우, 즉 stochastic 알고리즘을 생각해본다면

매번 다른 데이터를 이용하므로 local minima 에 빠질 위험은 적지만 학습시간이 너무 길어지므로 현대의 딥러닝 개발환경에 적합하지 않다고 생각할 수 있다.

이같은 배치사이즈와 gradinet descnet 속도 관계는 다음과 같은 그림으로 정리할 수 있다.

b. Data Parallelism 시에 GD는 어떻게 동작하나요?

미니배치에서 그래디언트 계산 방식에 대한 질문인데 사실 특별한 것은 없다. 위에서 말한 것처럼 매 iteration 마다 gradient 계산과 레이어 학습이 이루어진다.

아마 GPU 메모리 로드에 관련한 질문의 의도가 있는 듯한데 이 글에서는 하드웨어에 대해서 너무 깊이 다루지 않으므로 패스하자.

요즘 딥러닝 분야에서 학계를 넘어 사회적으로 가장 널리 회자되는 모델이 GPT-3가 아닌가 싶다.

나는 NLP 분야와는 거리가 멀지만, 최신 번역 모델의 기초가 되는 transformer가 무엇인지 간단하게 알아보기로 한다

시계열 분석에 대한 아이디어를 잘캐치하면 내 분야에도 적용할 기회가 있지않을까!

학습자료로는 서울대 윤성로 교수님의 강의영상을 활용했다

코시국 동안에 촬영하신 강의를 유투브로 배포하시는 교수님들이 많이 계시는데,

대학교나 딥러닝 회사 커뮤니티에 속하지 않은 나는 매우 감사할 따름이다.

1. Attention = learned allignment (between source and target)

번역 태스크에서 단어의 배열과 어순의 변경 등을 결정하기 위해서는 배열(allignment)정보를 가지는 벡터가 필요한데, 이것이 attention의 주요 역할이다.

이전의 seq2seq 모델에서는 배열정보를 가지기 위해 encoder에서 context vector를 계산했는데, encoder가 정보를 충분히 처리할 수 없는 (overloaded 되는) 문제가 발생한다. attention 을 도입함으로써 context vector computing 을 강화해서 더 좋은 성능을 가지게 되었다.

A traditional sequence-to-sequence model has to boil the entire input down into a single vector and then expands it back out. Attention avoids this by allowing the RNN processing the input to pass along information about each word it sees, and then for the RNN generating the output to focus on words as they become relevant.
Olah & Carter, 2016

이미지캡션 분야에서도 image-to-text 를 위해 집중해야할 이미지 영역을 강조하기 위해 이용된다

2. Attenetion 의 분류

Cross attention : 입력과 출력 시퀀스 사이에 어텐션을 생성한다. (works on different sequences)

Self attention : 시퀀스 내부에서 어텐션을 생성한다 (relates different positions of a single sequence to compute its representation)

Soft attention : 모든 인풋 데이터 패치에 대해 weight를 부여하고 전체의 average를 context vector로 가진다. 모델이 smooth and differntiable 하지만 연산량이 큰 단점이 있다

Hard attenetion : 선택된 일부 데이터 패치에 대해서만 weight를 부여한다. 연산량이 적고 속도가 빠르지만 selection 은 미분불가능한 stochastic한 방법이다.

Global attention : soft attention 의 개념과 유사함. 타겟을 생성하기 위해 모든 인풋을 살펴본다

Local attention : soft 와 hard attention 이 결합된 형태. 타겟 생성에 필요한 source 위치를 예측하고 그 주변에 window를 씌워서 타겟을 생성함.

3. Transformer 모델의 기본 연산과정 ("Attention Is All You Need" 논문의 모델)

기본적으로 인코더와 디코더 레이어를 쌓아서 many-to-many 맵핑을 수행하는 seq2seq 모델의 일종이다.

Encoder: 구조적으로 동일하고 가중치를 공유하지않는 6개의 레이어로 구성된다. 각각 2개의 sub-layer로 구성되어있는데 첫번째는 self-attention , 두번째는 feed-forward-net 이다. 

Decoder: 3개의 sub-layer로 구성되어있다. 첫번째는 self-attetion, 두번째는 encoder-decoder attention, 세번째는 feed-forward-net

트랜스포머 논문에서는 key와 value의 개념을 이용해서 다음과 같이 정의된 표현을 사용한다

Query: (projected) decoder hidden state

Key: (projected) encoder hidden state for attention weight computation

Value: (projected) encoder hidden state for context vector build

Context Vector = weighted sum of values

(위치의 weight 또는 score 값은 query 와 key를 내적해서 생성됨)

모델의 연산 과정

(그림은 https://jalammar.github.io/illustrated-transformer/ 에서 가져옴) 

(1) Query, Key, Value 를 생성

encoder에서 단어를 벡터로 word-embedding (1X512 벡터) 하고,

행렬 W_q, W_k, W_v 를 곱해서 

(2) 각 단어의 self-attention socre를 생성한다

위에서 정의한대로 score = query 와 key 를 내적한 값이다.

그 결과, 입력 시퀀스의 여러 단어(=key)에 대한 attention score 값이 생성된다

(3) attention score 를 normalize 한다

key 벡터의 길이가 64이므로, 제곱근인 8로 나누어주는 scaled-dot-product 를 적용한다. 정규화 를 통해 more stable gradient 를 얻는 장점이 있다

그리고 softmax를 적용해서 score를 probability 값으로 변환해준다

(4) self-attention layer의 output 를 계산한다

여기서 attention layer의 output (=context vector) 는 weighted sum of value vectors 이다.

즉 앞서 구한 softmax 값을 이용해서 z1 = v1*0.88 + v2*0.12 으로 계산된다

위의 과정을 행렬로 나타내면 다음과 같이 간단하게 표현할 수 있다

(5) multi-head attention

트랜스포머 모델은 각각 다른 방식으로 attention을 계산하기 위해서 8개의 attention head를 가진다.

그리고 multi-heads (z0, z1, ,,, z7) 를 하나로 concat한다.

(6) Positonal-Encoding 

각 단어가 문장에서 어디에 위치하는지 정보를 표현하는 벡터이다. 단어의 문장 내 위치와 다른 단어들과의 거리를 나타낼 수 있다. 본 논문에서는 20개 position에 대해 sin 함수를 이용해서 -1과 1사이의 값을 더한다 (물론 word-embedding 되었으므로 각 위치는 512개 차원의 값을 가진다)

(7) Add and Norm 서브레이어

Encoder에는 레이어를 스킵하는 residual connection 를 추가한다. 그림에서는 즉 x를 z에 더해주는 skip connection 이다. 그리고 그 결과를 layer normalization 를 수행한다.

즉 모든 Encoder 에서 Add and Norm 이라는 sub-layer 계산이 2번씩 추가되는 것으로 볼 수 있다.

(8) Decoder 레이어의 특징

인코더와 달리 encoder-decoder attention (=cross attention) 레이어를 가진다. 이 attention은 디코더가 인풋 시퀀스의 각 부분에 가중치를 가질 수 있도록 한다.

self-attention 계산과정에서 아직 생성되지않은 뒷 부분에 대한 attention을 가지지 않도록 수정된 구조(masked self-attention)를 가진다.

(9) 최종 결과물 생성하는 Logits and Softmax Layer

디코더의 최종 값은 float vector 꼴로 생성된다. 이를 단어로 변환하기 위해서 vocab size 수준의 매우 큰 Logits 로 바꿔야한다. 그리고 Logit vector 를 softmax 확률로 계산해서 가장 적합한 단어를 판정한다.

결과를 생성하는 방법으로는

① greedy decoding : softmax 확률이 가장 높은 단어를 추출한다

② beam search : beam size (=k) 개의 단어 후보를 동시에 고려하되, top beams(=t) 만큼의 결과만 저장해서 greedy 하게 진행한다. 

자 이제 "Attention Is All You Need"  논문에 나온 아래 트랜스포머 모델의 모든 요소를 다 이해했다!

교수님 감사합니다 !!

이후 강의에서 BERT와 GPT 모델에 대해서 설명해주시는데

번역 모델들에 대해 너무 자세히 알아볼 필요는 없으므로 트랜스포머 정리는 여기까지 !

### 추가로 참고하면 좋은 자료

ICML2019 tutorial : Attention in Deep Learning